Золотое сечение прямоугольника — разъяснение понятия — Paradox Review — Medium
Узнайте все о «золотом сечении прямоугольника» в новой публикации на Paradox Review в Medium. Этот увлекательный материал разъясняет понятие золотого сечения прямоугольника и его роль в искусстве и дизайне. Погрузитесь в мир гармонии и баланса!
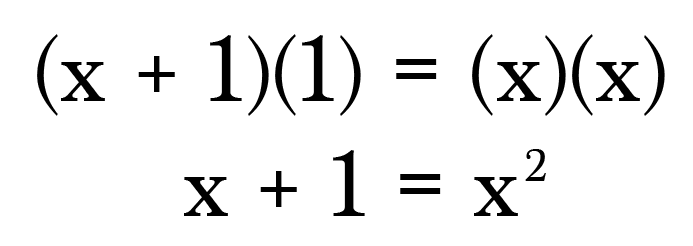
Что такое «золотое сечение»?
На протяжении веков «золотое сечение» считается самым прекрасным соотношением в искусстве и архитектуре.
«Золотое сечение», называемое также «золотая пропорция» или «золотое соотношение», было обнаружено во многих самых знаменитых творениях человечества — от древнегреческого Парфенона до творений Сальвадора Дали. Возможно, вы уже читали на эту тему статью «Нереализованное влияние золотого сечения».
Не важно, считаете ли вы, что эта божественная пропорция является поистине знамением красоты или просто предвзятым выбором, но, без сомнения, это одно из самых интригующих чисел в мире. Поэтому, сейчас мы поговорим о математической основе «золотого сечения».
Впервые о «золотом сечении» упоминает древнегреческий математик Евклид около 300 лет до нашей эры. В шестой книге своего трактата «Начала» Евклид дает определение «золотого сечения». Он поручает нам взять отрезок линии и разделить его на два меньших сегмента так, что отношение всей линии (a + b) к отрезку a будет таким же, как отношение отрезка a к сегменту b:
Что эквивалентно пропорции:
Евклид использовал «золотое сечение» для построения правильного пятиугольника. Отношение диагонали правильного пятиугольника к его стороне равно золотому сечению. Правильный пятиугольник (пентагон) еще называют «золотой пятиугольник».
Золотой прямоугольник
«Золотое сечение» часто представляют как «Золотой прямоугольник» — прямоугольник с отношением длин сторон примерно .
Этот прямоугольник обладает тем свойством, что если от него отрезать квадрат, то снова получится золотой прямоугольник меньшего размера и так до бесконечности.
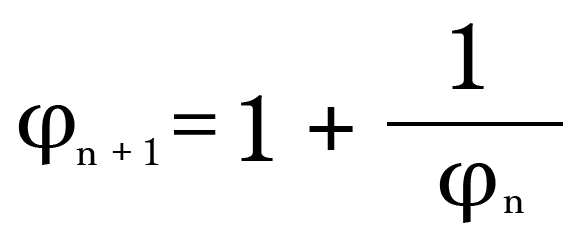
На самом деле, соотношение сторон «золотого прямоугольника» — это иррациональное значение 1,618034…, т.е. бесконечная десятичная дробь, не имеющая периода.
Это число и есть пропорция «золотого сечения», оно обозначается греческой буквой Фи в честь древнегреческого скульптора и архитектора Фидия, мастера, воплотившего его в своих работах.
Решение «золотой пропорции»
Чтобы найти значение 1,618034…, мы должны решить пропорцию, показанную выше. Для простоты предположим, что b = 1 и a = x и найдем решение для x.
Шаг 1. Сделаем перекрестное умножение:
Шаг 2. Приведем уравнение к 0:
Шаг 3. Решим квадратное уравнение:
Поскольку мы работаем с длинами, нам нужно только положительное решение:
Решение найдено! «Золотое сечение» выражается, как дробь.
Для проверки подставим a = 1.618 и b = 1, чтобы убедиться, что наша пропорция верная:
Обратите внимание, как интересно: мы можем написать «золотое соотношение» при помощи самого себя. Это потрясающе!
Что эквивалентно:
Пойдем дальше… Заменим φ = 1 + 1 / φ для φ в знаменателе:
И еще дальше!
Мы могли бы продолжать делать это бесконечно. Оказывается, «Золотое сечение» может быть записано как бесконечная цепная дробь.
«Золотое сечение» и числа Фибоначчи
Мы можем использовать непрерывную дробь, чтобы раскрыть связь «золотого сечения» с последовательностью Фибоначчи.
Для начала мы немного изменим нашу бесконечную дробь — добавим индексы, чтобы показать, как следующее значение φ(n+1) может быть получено из предыдущего значения φ(n).
Так как это бесконечная цепная дробь, с ростом n искомое значение приближается к истинному значению φ.
Теперь допустим, что φ(0) = 1 и найдем φ(1).
Продолжим вычислять следующеезначение — φ(2)
И далее… φ(3), φ(4)…
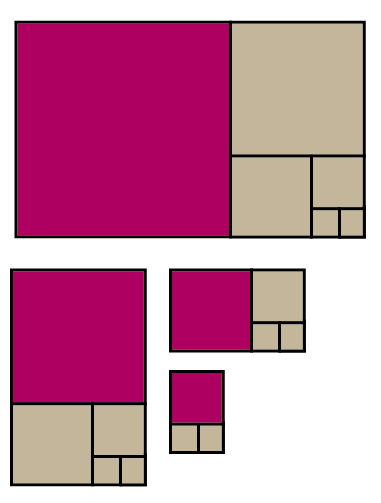
Посмотрите! Это же последовательность Фибоначчи! Каждое приближение — это отношение двух соседних чисел Фибоначчи.
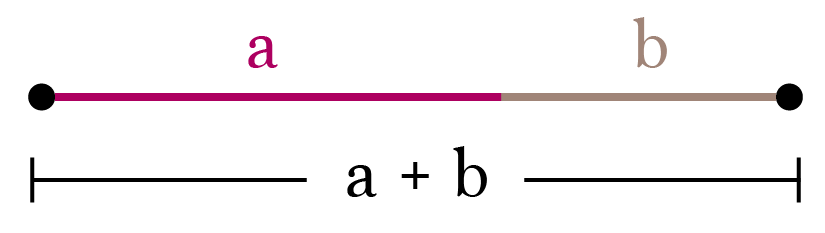
По мере продвижения к каждому новому последовательному вычислению мы обнаруживаем, что наше искомое значение все ближе и ближе приближается к его истинному «Золотому сечению».
На девятом члене последовательности Фибоначчи мы уже получаем значения «золотого сечения», с тремя верными цифрами после запятой.
В самом деле, limit F(n+1)/F(n) при n→∞ (где F(n) и F(n+1) представляют n и n+1 числа в последовательности Фибоначчи) сходится к φ.
Если визуализировать этот процесс, то мы увидим, как последовательность Фибоначчи создает прямоугольники всё ближе и ближе к «Золотому прямоугольнику».
Хотя в мире дизайна продолжаются споры о том, является ли «золотое сечение» оптимальной пропорцией или нет, можно с уверенностью сказать, что оно математически совершенно и не перестает нас удивлять.
На чем основано золотое сечение?
Золотое сечение — это математическое соотношение между двумя величинами, при котором отношение меньшей величины к большей равно отношению большей величины ко всей величине. Это соотношение имеет константу, которая приблизительно равна 1,61803398875 (обозначается символом φ). Золотое сечение широко применяется в искусстве, архитектуре, дизайне и других областях для создания более гармоничных и пропорциональных форм. Оно также имеет математическое и физическое значение в теории чисел, теории вероятности, теории динамических систем и других областях науки.